Drehregler verwenden
Die Messung einer variablen, (quasi-)analogen Spannung eröffnet neue Möglichkeiten, da die Eingabewerte nun viel differenzierter sind als bei einem Taster, bei dem die Eingabe nur aus “0” oder “1” b...
Anwendungen der Spannungsmessung
Jede Messung mit einem Mikrocontroller basiert darauf, dass eine Umweltgröße, die gemessen werden soll, auf eine messbare Spannung zurückgeführt wird, die dann vom Mikrocontroller verarbeitet wird. In diesem Abschnitt wird an drei Beispielen erkundet, wie man aus der Spannung, die an analogen Eingängen gemessen wird, wieder die Umweltgröße ermittelt. In einem zusätzlichen Abschnitt wird gezeigt, wie man eine Regression durchführt, um einen funktionalen Zusammenhang zu ermitteln.
Helligkeit messen mit einem LDR
Ein LDR. Die Helligkeit bestimmt unseren Tages- und Jahresrhythmus: Wenn es dunkel wird, schlafen wir (oder gehen feiern) und wenn es hell wird, stehen wir wieder auf und unternehmen etwas. Es is...
Temperatur messen mit einem NTC
Ein NTC. Nicht nur die Helligkeit beeinflusst unseren Alltag, sondern auch die Temperatur. Ganz allgemein ist die Temperatur eine wichtige Größe, die bei vielen Anwendungen eine Rolle spielt und...
Werkzeug: Regression durchführen
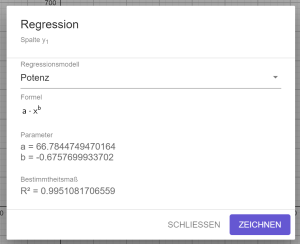
In diesem Abschnitt wird gezeigt, wie man mit verschiedenen Werkzeugen eine Regression durchführt, um einen funktionalen Zusammenhang zu ermitteln. Als Beispiel dienen Daten zur Helligkeit und zur S...